3D Meshing

3D Meshing (Poisson reconstruction)

This tool allows you to reconstruct a triangle mesh from any point cloud. Unlike uniform or multiresolution meshing, this technique does not need the input cloud to be structured. Also, unlike meshing from predefined view and topographic meshing, this technique is not view-dependent. It reconstructs a connected, watertight surface taking as constraints the points' positions and orientations (normals).

It’s suggested to reconstruct a convex (closed) surface.

If you need to work with a set of point clouds (structured or not), it’s better to lump them together in an unstructured point cloud using the Level 3D density of clouds command.

In the 3D Meshing Dialog you can manage some parameters' presets to obtain a best fitted mesh.

Adding color

In the first parameter box of the dialog, you can select by the flag whether the output mesh should be colored or not, and which of the input cloud's color layers should be used.

Resulting mesh resolution

While meshing from predefined view is interpolative, this reconstruction technique is approximate: it creates a triangulation that approximates the surface described by the points. In the second parameter box, you can specify how many details you want to preserve in the output mesh. The higher the resolution (from Low to High), the finer the details that will be reconstructed, and also the heavier the mesh file and rendering time.

Input cloud noise level

In the third parameter box, you can take into account the cloud smoothness, according to the point cloud noise.

If your cloud represents clean construction data, then select Low. If, however, your cloud contains noisy territorial data, then select High.

Size of holes to close and islands to remove

In the last parameter box, you can specify the size of the holes that are going to be closed in the mesh, and the size of the “islands” (small disconnected components that may have been created) to be removed (or not). The size is computed as ratio between the area of the hole/island and the area of the whole mesh.

Raw parameters

By clicking the Raw parameters button, a new dialog expliciting all the parameters will appear.

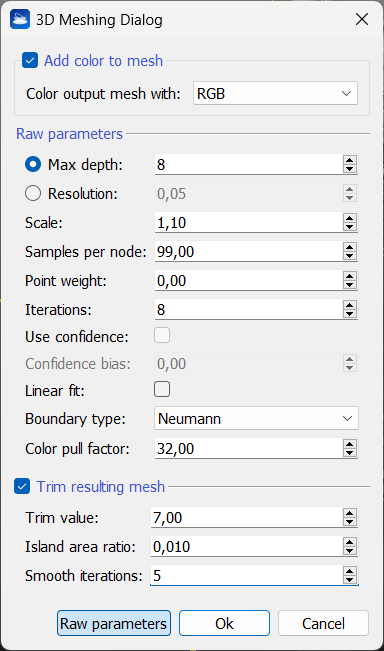
Max depth: it is the maximum depth of the tree that will be used for surface reconstruction, defining the resolution of the final mesh. Running at depth d corresponds to solving on a grid whose resolution is no larger than 2^d x 2^d x ... Note that since the reconstructor adapts the octree to the sampling density, the specified reconstruction depth is only an upper bound.
Generally, the bigger is the value, the better is the reconstruction - preserving more details - but more time is necessary. For almost all uses keep the value between 8 and 12, and not to increase it more than 20 because it is usefulness and no details are added.
Resolution: as an alternative to the Max depth parameter, the resolution can be directly set changing this value defining the density of the initial point cloud.
Scale: it specifies the ratio between the diameter of the cube used for reconstruction and the diameter of the samples' bounding cube. The default value is 1.1.
Samples per node: it defines how to smooth the final mesh. SPN is the minimum number of sample points that should fall within an octree node as the octree construction is adapted to sampling density.
For noise-free samples, small values in the range[1.0-1.5] can be used. For more noisy samples, larger values in the range [15.0-20.0] may be needed to provide a smoother, noise-reduced reconstruction.
Point weight: it defines the capacity of the algorithm to preserve the details.
If you have small disalignments or "double surfaces" in the point clouds, it's suggested to set small values, from 0 until 4. Otherwise set 4 or larger values.
Iterations: it specifies the number of Gauss-Seidel relaxations to be performed at each level of the hierarchy. The default value for this parameter is 8.
Use confidence: flagging this parameter, the quality of the points (defined by the confidence value, if present in the initial point cloud) will be used to obtain a better reconstruction. The normals are here normalized using the confidence values.
Confidence bias: it specifies the exponent to be applied to a point's confidence to bias the resolution at which the sample contributes to the linear system. Points with lower confidence are biased to contribute at coarser resolutions. The default value for this parameter is 0.
Linear fit: enabling this flag has the reconstructor use linear interpolation to estimate the positions of iso-vertices.
Boundary type: it specifies the boundary type for the finite elements. choosing between Free boundary constraints, Dirichlet boundary constraints and Neumann boundary constraints. The default value for this parameter is Neumann.
Color pull factor: if the input points have additional data as color, that is to be sampled at the output vertices, this value specifies the relative importance of finer data over lower data in performing the extrapolation. The default value for this parameter is 32.

By flagging Trim resulting mesh it is possible to reduce the output mesh extents so as to match as best the input cloud extents. The triangles with vertices having the lowest density values, that are the farthest from the input cloud, will be detected and removed.

Trim value: it specifies the value for mesh trimming. The subset of the mesh with density value less than the trim value is discarded.
Island area ratio: it specifies the area ratio that defines a disconnected component as an "island". Connected components whose area, relative to the total area of the mesh, are smaller than this value will be merged into the output surface to close small holes, and will be discarded from the output surface to remove small disconnected components. The default value 0.001.
Smooth iterations: it values the number of umbrella smoothing operations to perform on the density cloud before trimming. The default value is 5.

NOTE: the algorithm is based on the Poisson Surface Reconstruction code developed by Misha Kazhdan et al.